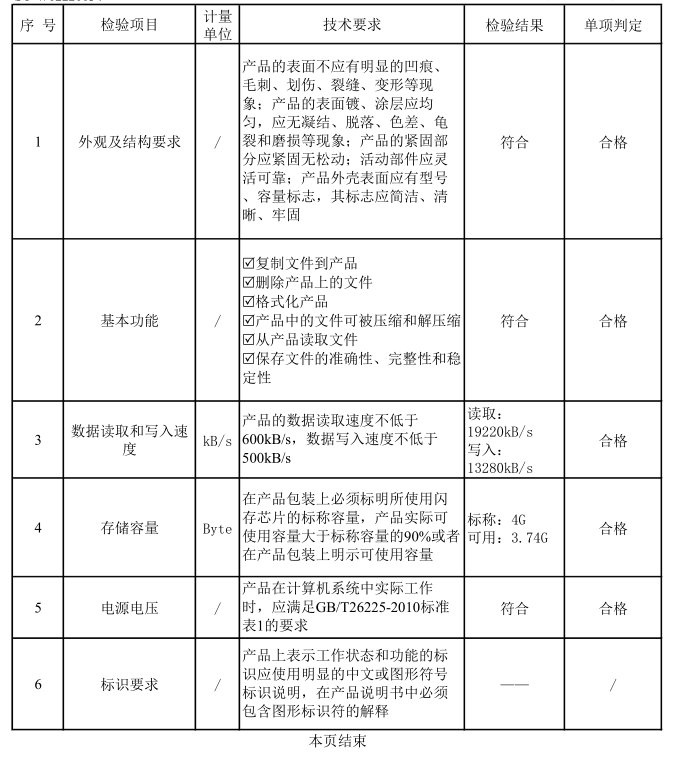
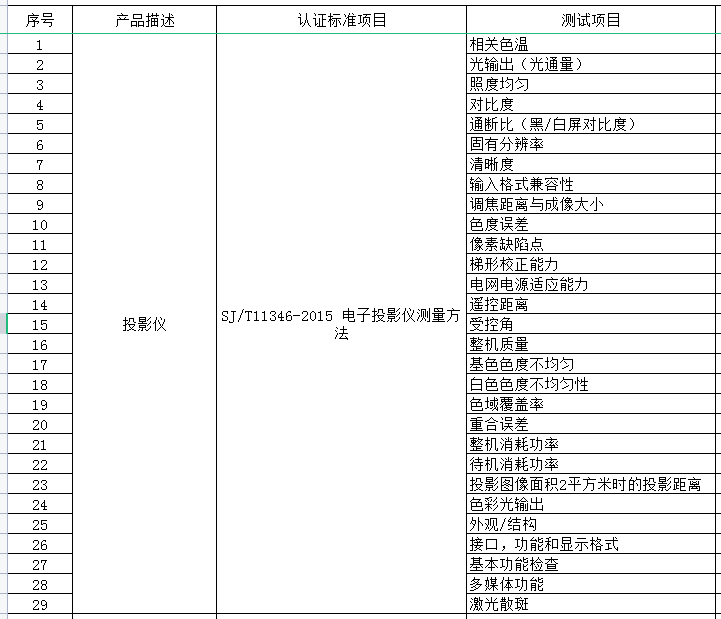
摄像头检测认证周期多久
 |
更新时间
2024-07-13 08:06:00
价格
请来电询价
联系电话
400-108-6070
联系手机
18682191300
联系人
李经理
立即询价
|
详细介绍
通常，镜头和图像传感器都可以被视为线性系统，因此当从镜头捕获图像时从相机传感器发出的信号 可以通过输入信号的卷积 和点扩散函数 来描述：
由卷积定理可知，两个函数在空间域的卷积等价于它们的傅里叶变换在空间频域的乘积。 点扩散函数（PSF，在第 4 章中定义）的傅里叶变换称为光学传递函数（optical transfer function, OTF）。 由于点扩散函数提供了有关输入信号空间修改的信息，因此 OTF 将描述系统将如何修改不同的空间频率。 在数学上，OTF、 和点扩散函数之间的关系写为
这表明 OTF 是复数，即：
其中 描述了输入信号的幅度将如何被系统修改，而 描述了信号的相位将如何变化。 对于不会发生输入平移的对称 PSF（即 PSF 是偶函数），OTF 将是实数，相位函数 的可能值是零或 的倍数 . 对于奇数倍数，OTF 将为负值，在这种情况下会发生信号的相位反转。 例如，散焦就是这种情况，它的 PSF 可以用柱面函数来描述.
其中是一阶 Bessel 函数 (Arfken, 1985)。该函数与西门子星形目标的图像一起显示在图 6.17 中，当视线从边缘移动到中心时可以清楚地看到相位反转，从而观察到越来越高的空间频率。
由卷积定理可知，两个函数在空间域的卷积等价于它们的傅里叶变换在空间频域的乘积。 点扩散函数（PSF，在第 4 章中定义）的傅里叶变换称为光学传递函数（optical transfer function, OTF）。 由于点扩散函数提供了有关输入信号空间修改的信息，因此 OTF 将描述系统将如何修改不同的空间频率。 在数学上，OTF、 和点扩散函数之间的关系写为
这表明 OTF 是复数，即：
其中 描述了输入信号的幅度将如何被系统修改，而 描述了信号的相位将如何变化。 对于不会发生输入平移的对称 PSF（即 PSF 是偶函数），OTF 将是实数，相位函数 的可能值是零或 的倍数 . 对于奇数倍数，OTF 将为负值，在这种情况下会发生信号的相位反转。 例如，散焦就是这种情况，它的 PSF 可以用柱面函数来描述.
其中是一阶 Bessel 函数 (Arfken, 1985)。该函数与西门子星形目标的图像一起显示在图 6.17 中，当视线从边缘移动到中心时可以清楚地看到相位反转，从而观察到越来越高的空间频率。
相关产品
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
请联系我们询价
产品分类
联系方式
- 电 话： 400-108-6070
- 业务发展部： 李经理
- 手 机： 18682191300
- 微 信： 18682191300
公司官网
